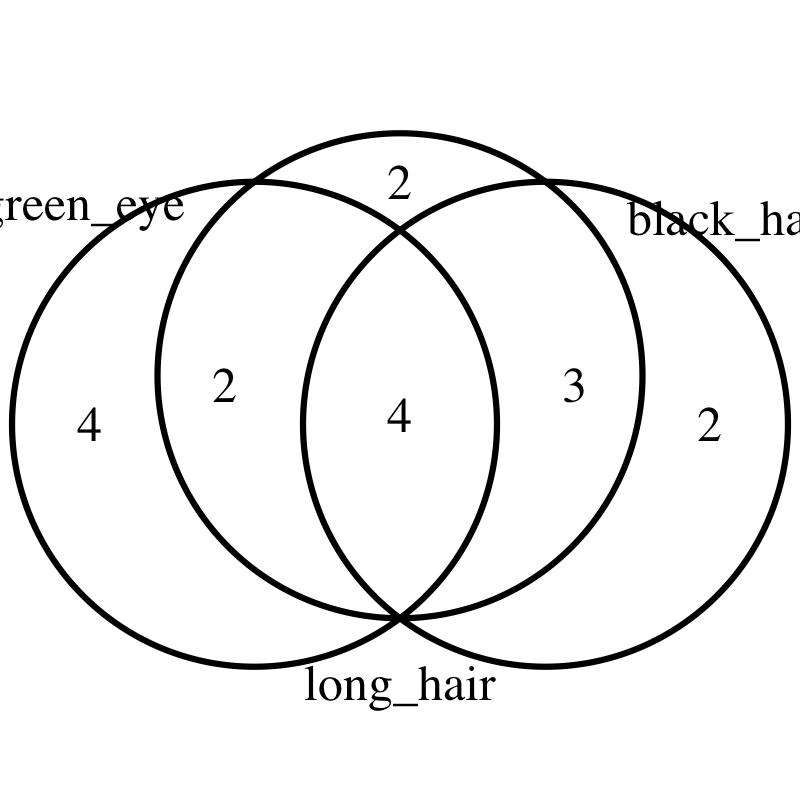
Overview #
Venn diagrams are used to visually show commonalities between groups.
Usually, distinct groups are represented in Venn diagrams as circles or ellipses. Where these shapes overlap represent commonalities between groups.
Oftentimes, the different parts of a Venn diagram are labeled with the groups' defining features and with counts of the number of things that fall within each part of the Venn diagram.
So if there’s a circle for Group A, and another circle for Group B, and there’s some overlap of those two circles, where there is overlap represents individuals that are part of both Group A and Group B.
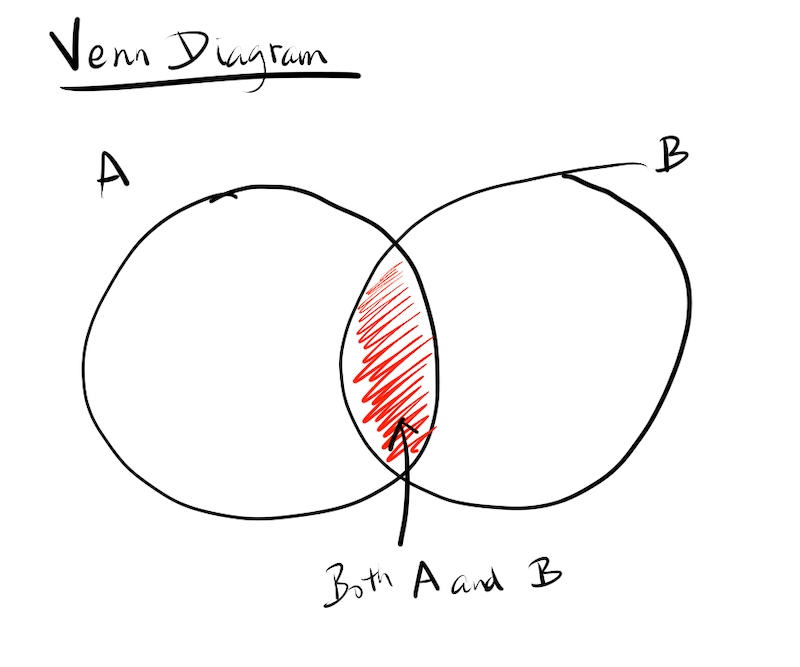
Venn diagrams are also called set diagrams or logic diagrams. I’ve been saying “group” because it’s pretty informal and colloquial.
In more precise terms, these “groups” of things are referred to as “sets” in math or other data practices. So in the above example, Group A can be thought of as Set A, which is the set of things that have the attribute A.
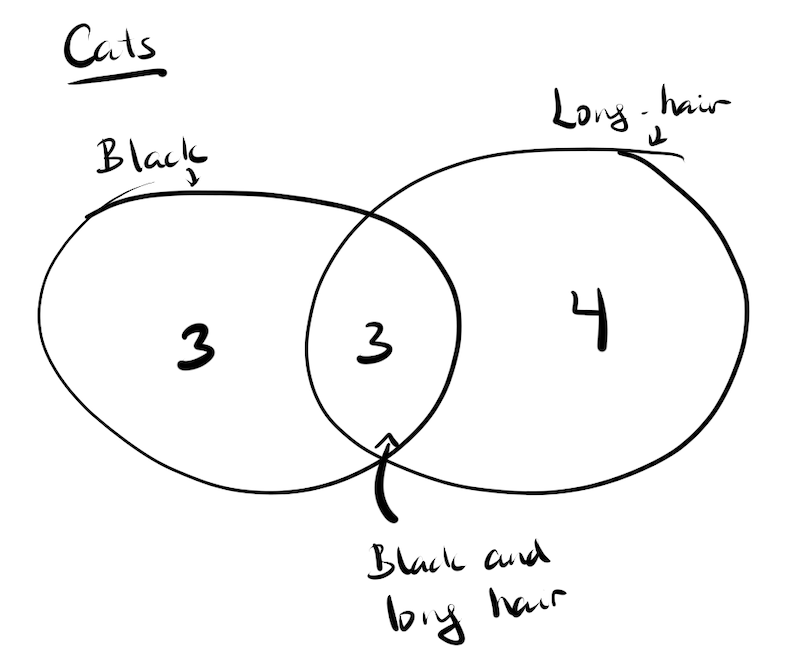
Let’s use a more tangible (but maybe a bit silly) example. Let’s say we have 10 cats, 3 of them are black, 4 of them have long hair, and 3 of them are both black and have long hair. The Venn diagram for that arrangement would look like this:
Set Theory #
Without going too deep, it helps to borrow precise language from the space of set theory, the field of mathematics that studies sets.
So here are some terms:
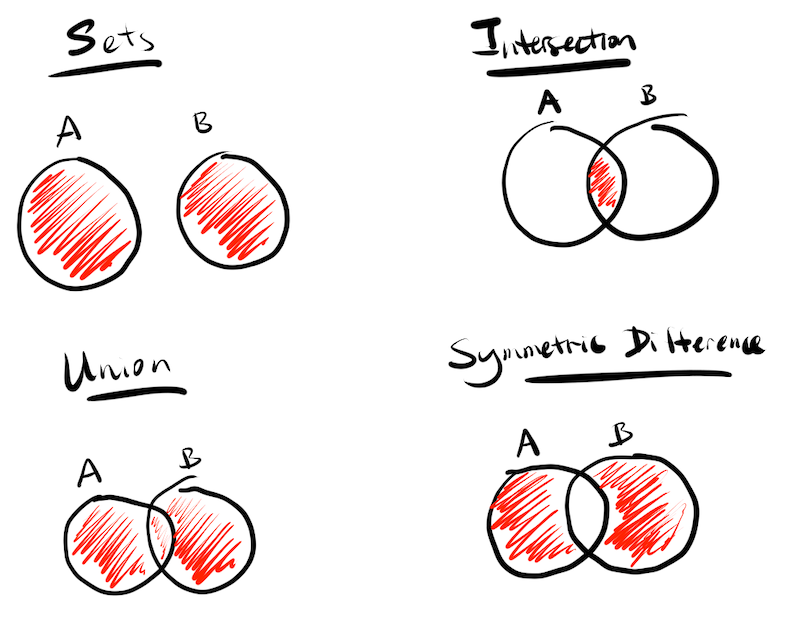
- Thing - this is a very non-technical term, I’m using it here to refer to a unique observation.
- Set - A collection of things that share some common attribute.
- Union - All the things under consideration.
- Intersection - the bunch of things that fit in more than one set.
- Symmetric difference of two sets - if we’re looking only at two sets, then this refers to everything that is not an intersection of the two sets.
Data #
The data required for a Venn diagram needs to be structured to convey the number of observations that are contained within different groups. There are several different ways to do this.
The original data might start as very discrete records of individual observations. Oftentimes, this original data needs to be transformed to be a more condensed form that doesn’t have all that raw detail.
For instance, the original data might include details about a bunch of cats. The features about those cats might be things like:
- Black or not
- Long hair or not
- Green-eyed or not
So a dataframe might look like this:
| black_hair | long_hair | green_eye |
|---|---|---|
| FALSE | TRUE | TRUE |
| TRUE | TRUE | FALSE |
| FALSE | TRUE | FALSE |
| TRUE | FALSE | FALSE |
| TRUE | TRUE | TRUE |
| FALSE | FALSE | FALSE |
| FALSE | FALSE | TRUE |
| TRUE | TRUE | FALSE |
| FALSE | TRUE | FALSE |
| FALSE | FALSE | FALSE |
| TRUE | TRUE | TRUE |
| TRUE | FALSE | FALSE |
| FALSE | FALSE | TRUE |
| FALSE | FALSE | TRUE |
| TRUE | TRUE | FALSE |
| TRUE | TRUE | TRUE |
| FALSE | FALSE | TRUE |
| TRUE | TRUE | TRUE |
| FALSE | TRUE | TRUE |
| FALSE | FALSE | FALSE |
This is a logical table, where TRUE means an observation has a specific feature. So any row that has TRUE under BLACK_HAIR refers to a cat that has black hair, any row that has FALSE under BLACK_HAIR is a cat that doesn’t have black hair.
Oftentimes, TRUE is represented as 1 and FALSE is represented as 0.
There are other ways to show this sort of detail.
The data that is used to generate a Venn diagram can often be reduced to a simpler data structure by counting the number of observations that do or do not have some particular combination of features.
| black_hair | long_hair | green_eye | count |
|---|---|---|---|
| FALSE | FALSE | FALSE | 3 |
| FALSE | FALSE | TRUE | 4 |
| FALSE | TRUE | FALSE | 2 |
| FALSE | TRUE | TRUE | 2 |
| TRUE | FALSE | FALSE | 2 |
| TRUE | TRUE | FALSE | 3 |
| TRUE | TRUE | TRUE | 4 |
R #
There are a number of different packages within R that can be used to generate Venn diagrams.
ggVennDiagram #
Package ggVennDiagram can generate Venn diagrams for 2-7 sets (though too many sets in a Venn diagram can be a bit overwhelming to read) and builds upon ggplot2.
First, load it up:
As input, the ggVennDiagram() function takes lists of lists (note: not a dataframe), where the lists represent the specific records that fit within a particular group.
In R, we can use the which() function to determine the index (or record position) of those that are TRUE.
which(black_hair)
## [1] 2 4 5 8 11 12 15 16 18
which(long_hair)
## [1] 1 2 3 5 8 9 11 15 16 18 19
which(green_eye)
## [1] 1 5 7 11 13 14 16 17 18 19
venn_list_dat <- list(
black_hair = which(black_hair),
long_hair = which(long_hair),
green_eye = which(green_eye)
)
venn_list_dat
## $black_hair
## [1] 2 4 5 8 11 12 15 16 18
##
## $long_hair
## [1] 1 2 3 5 8 9 11 15 16 18 19
##
## $green_eye
## [1] 1 5 7 11 13 14 16 17 18 19
With the data now properly structured, we can generate a Venn diagram with ggVennDiagram.
ggVennDiagram(venn_list_dat)
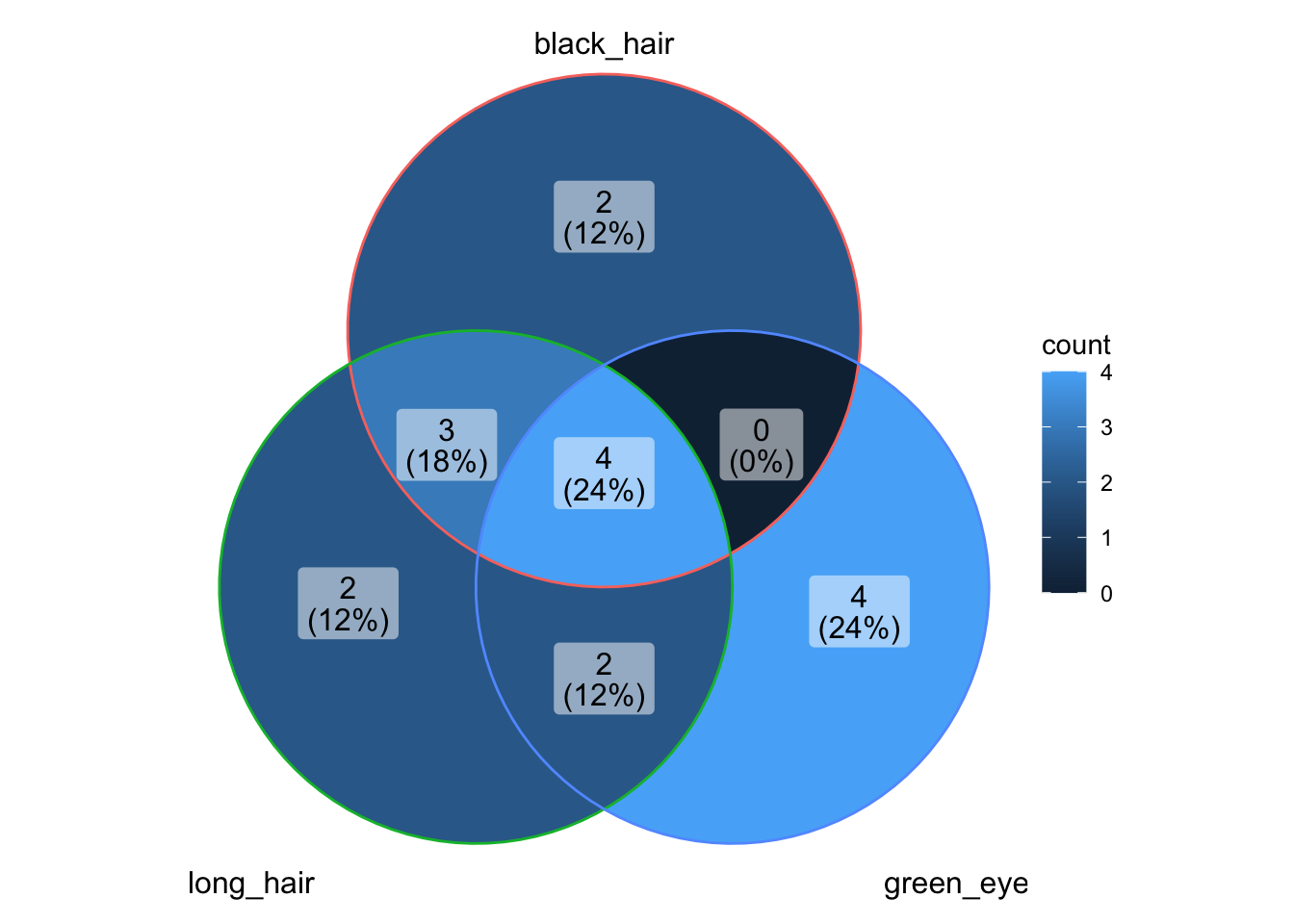
Since ggVennDiagram is built on top of ggplot2, we can use the functions available through ggplot2 to modify the plot.
ggVennDiagram(
venn_list_dat
) +
scale_fill_gradient(low = "red", high = "blue") + # change the fill colors
theme(legend.position = "bottom") + # move the legend to the bottom
labs(
title = "A Venn Diagram about cats" # give the plot a label
)
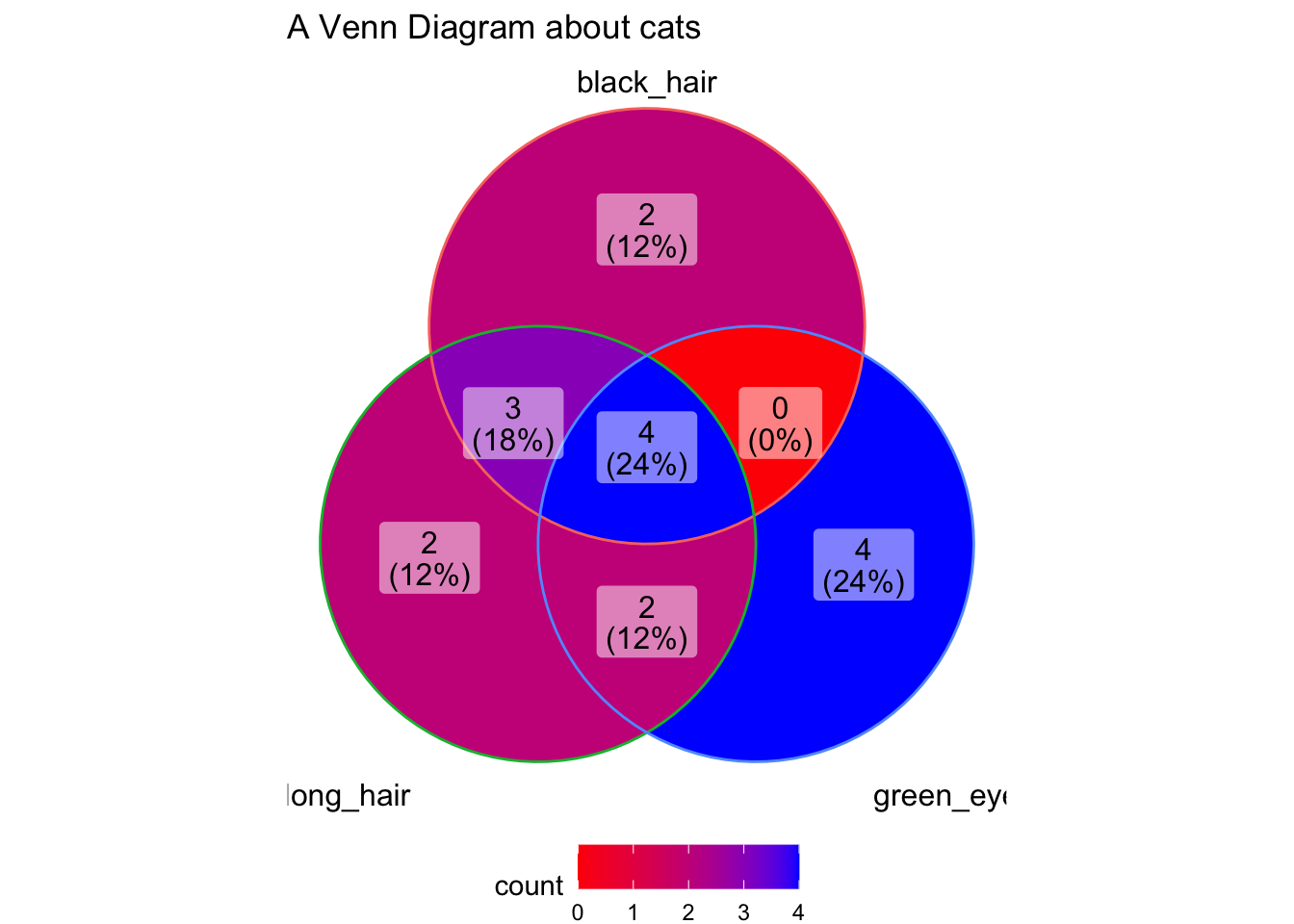
For more details about ggVennDiagram, check out this article.
ggvenn #
Package ggvenn can generate Venn diagrams using both list and dataframes as inputs.
# install.packages("ggvenn") # run if the packge hasn't already been installed
library(ggvenn)
If the data is a lists of lists, then the elements of the underlying lists should be unique identifiers for each thing.
venn_list_dat
## $black_hair
## [1] 2 4 5 8 11 12 15 16 18
##
## $long_hair
## [1] 1 2 3 5 8 9 11 15 16 18 19
##
## $green_eye
## [1] 1 5 7 11 13 14 16 17 18 19
With ggvenn, the Venn diagram can be selectively generated by specifying the sets to be included.
Here we’re only including two of the three sets in the available data.
ggvenn(
venn_list_dat,
c("black_hair", "long_hair")
)
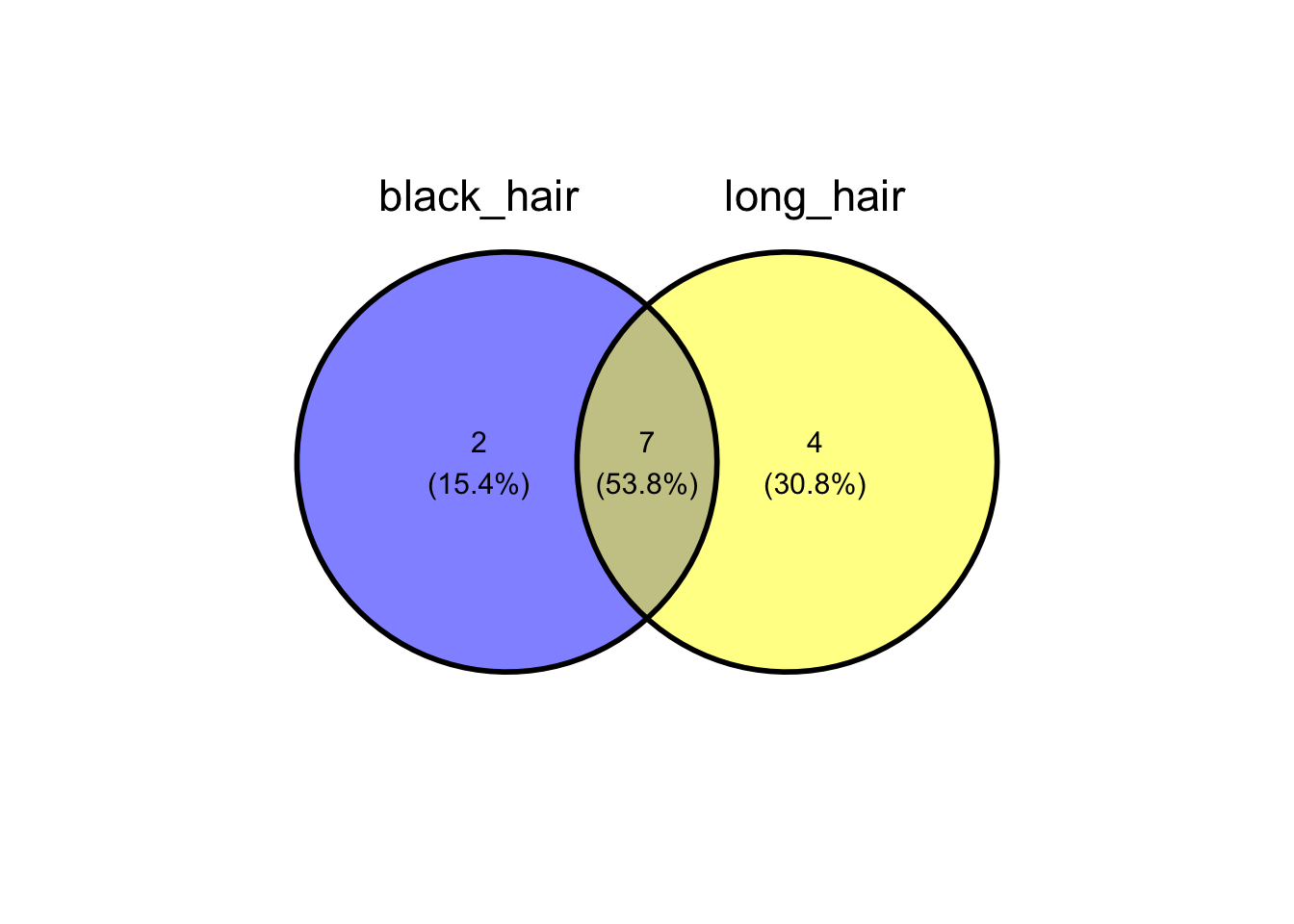
And now, we’re specifying all three available set.
ggvenn(
venn_list_dat,
c("black_hair", "long_hair, green_eye")
)
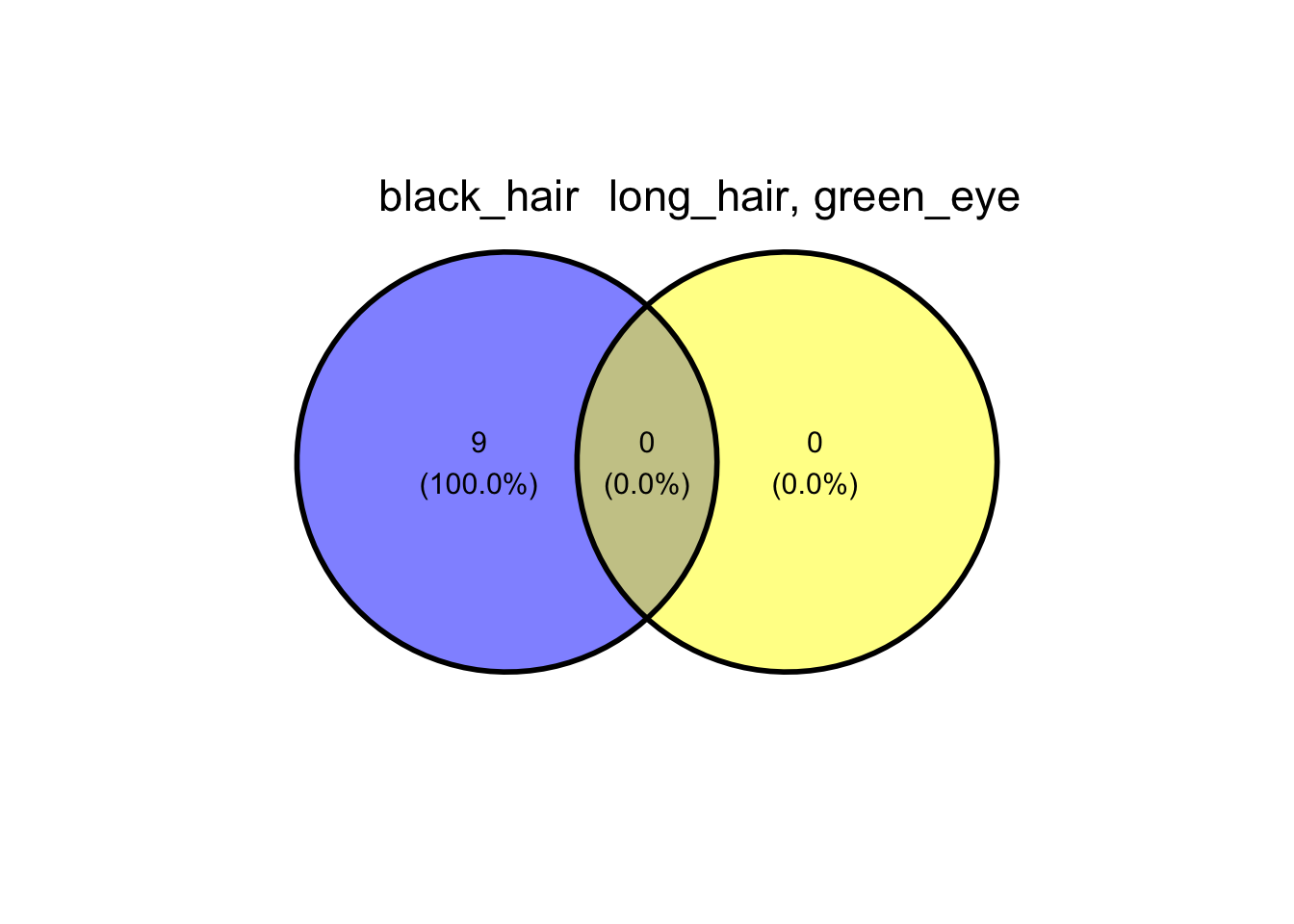
ggvenn can also utilize data in the form of a dataframe made up of columns of logical data (i.e., TRUE or FALSE).
cat_dat
## black_hair long_hair green_eye
## 1 FALSE TRUE TRUE
## 2 TRUE TRUE FALSE
## 3 FALSE TRUE FALSE
## 4 TRUE FALSE FALSE
## 5 TRUE TRUE TRUE
## 6 FALSE FALSE FALSE
## 7 FALSE FALSE TRUE
## 8 TRUE TRUE FALSE
## 9 FALSE TRUE FALSE
## 10 FALSE FALSE FALSE
## 11 TRUE TRUE TRUE
## 12 TRUE FALSE FALSE
## 13 FALSE FALSE TRUE
## 14 FALSE FALSE TRUE
## 15 TRUE TRUE FALSE
## 16 TRUE TRUE TRUE
## 17 FALSE FALSE TRUE
## 18 TRUE TRUE TRUE
## 19 FALSE TRUE TRUE
## 20 FALSE FALSE FALSE
Each logical column is interpreted as a set.
The logical columns can be specified to generate Venn diagrams in ggvenn.
ggvenn(cat_dat, c("black_hair", "long_hair"))
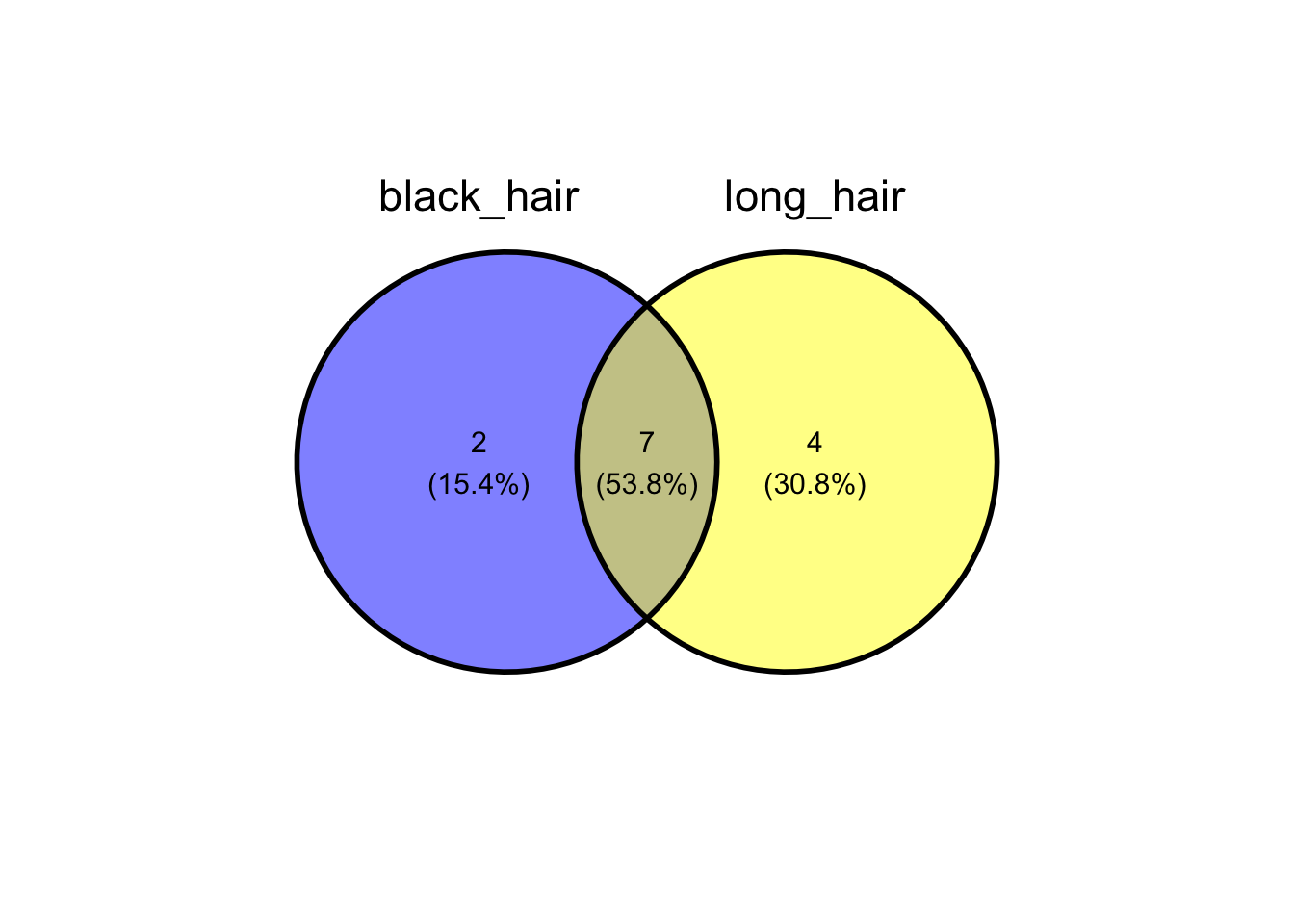
Additional sets can be added explicitly.
ggvenn(cat_dat, c("black_hair", "long_hair", "green_eye"))
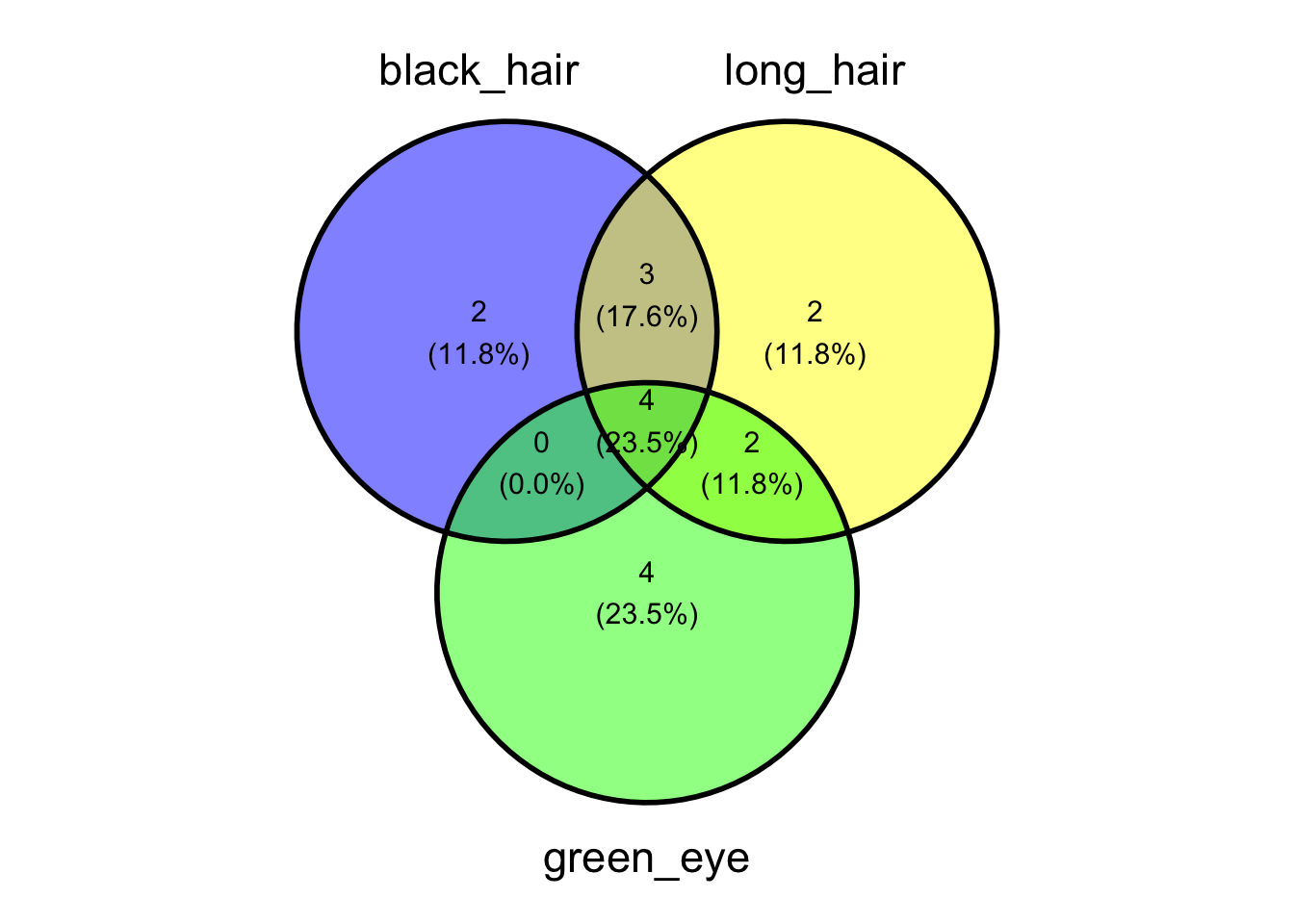
VennDiagram #
The VennDiagram package can also be used to generate Venn diagrams. The functions available through the VennDiagram package can take as input list of lists, or the user can explicitly specify the sizes of the areas.
This package is not premised on ggplot2.
# install.packages("VennDiagram") # run this if the package isn't already installed
library(VennDiagram)
A single-set Venn diagram (really, just a circle) can be generated using the draw.single.venn() function, with a specification of the area size. Note that a grid.newpage() is first required to set up a page for rendering.
grid.newpage()
draw.single.venn(area=7)
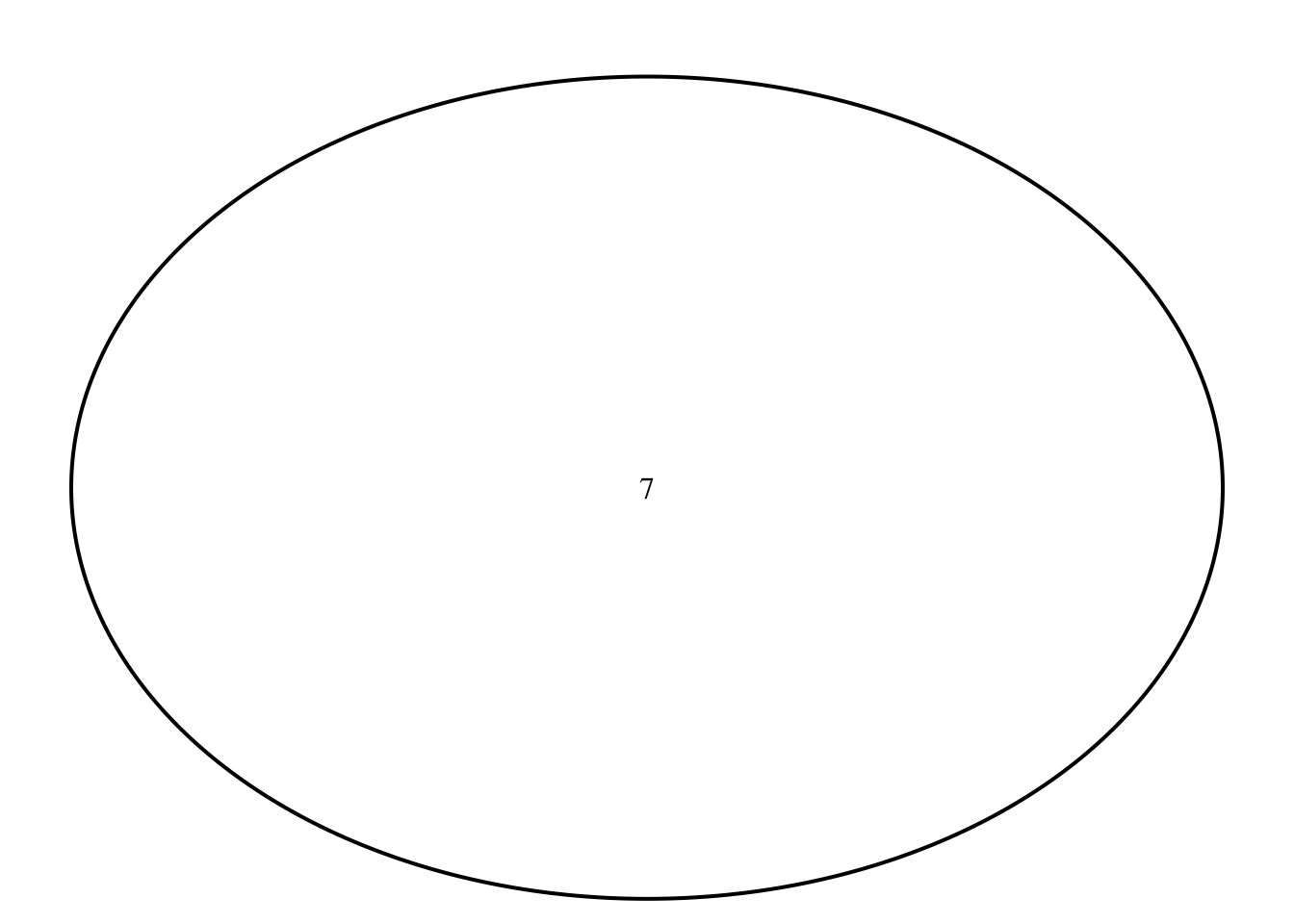
## (polygon[GRID.polygon.174], polygon[GRID.polygon.175], text[GRID.text.176], text[GRID.text.177])
A two-set Venn diagram is generated using the draw.pairwise.venn() function, where area* specifies the size of the distinct sets, and cross.area specifies the intersection. Note that the circles are not the same size; they are instead proportional to the specified area.
grid.newpage()
draw.pairwise.venn(area1=9, area2=11, cross.area=7)
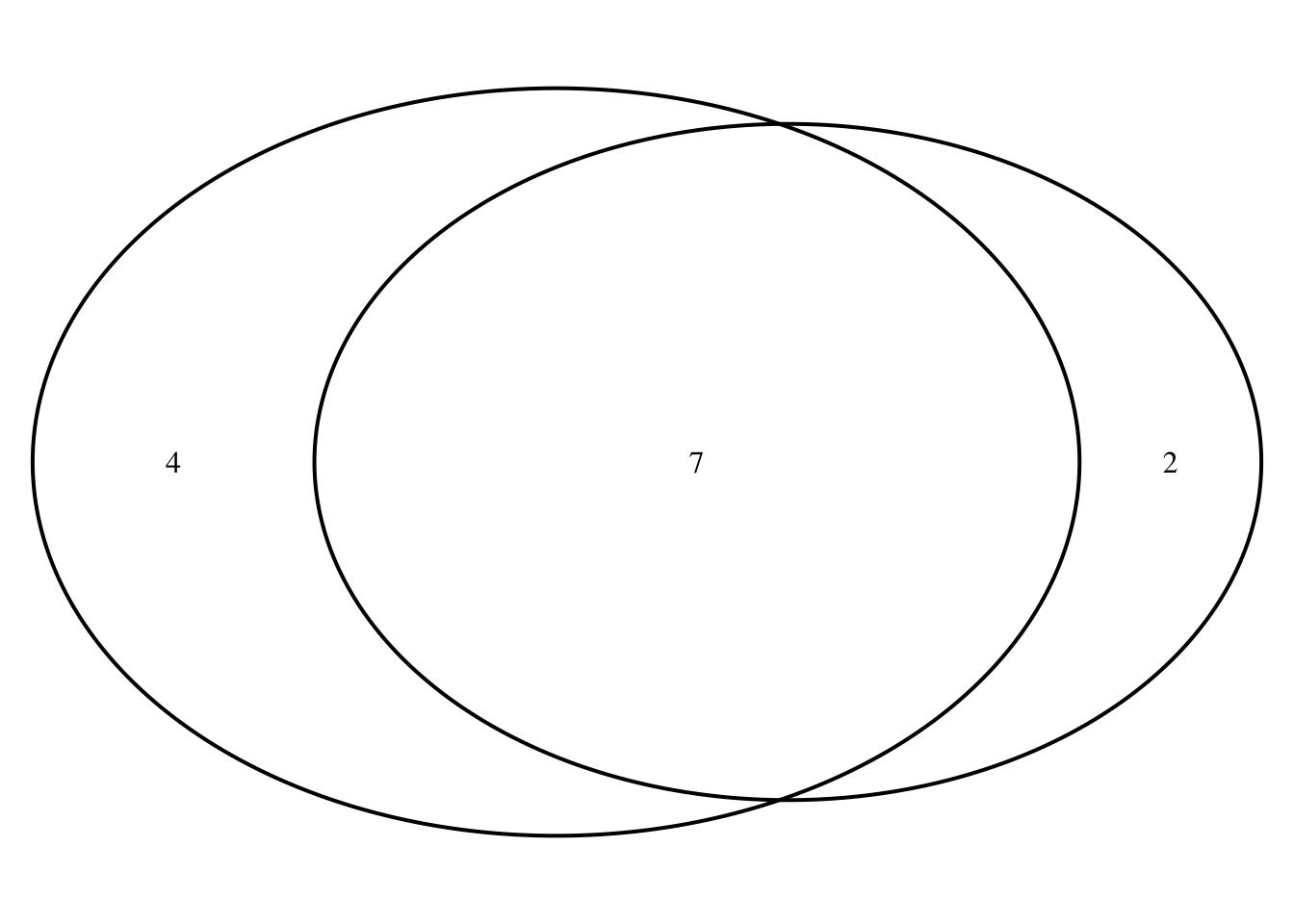
## (polygon[GRID.polygon.178], polygon[GRID.polygon.179], polygon[GRID.polygon.180], polygon[GRID.polygon.181], text[GRID.text.182], text[GRID.text.183], text[GRID.text.184], text[GRID.text.185], text[GRID.text.186])
With VennDiagram, a three-set Venn diagram can be generated using the draw.triple.venn() function, with specifications for area and intersection size.
Intersections are specified in the form n<set1><set2>.... For instance, the intersection of sets 1 and 2 is specified with the parameter, n12, the intersections for sets 2 and 3 is specified with n23, and the intersections for three sets is specified with n123, and so on. This approach is highly manual, prone to error, and is inadvisable for use.
Another function available in the VennDiagram package is the venn.diagram() function, which directly outputs a Venn diagram to a file.
venn.diagram(
x = venn_list_dat,
filename = 'img/vd_venn.png',
# Output features
imagetype="png" ,
height = 800 ,
width = 800 ,
resolution = 300,
compression = "lzw",
)
## [1] 1
Note the specification of image features. Without these parameters specified, the output file ends up being pretty big.